相対論 (1) - 定数、換算式 -¶
定数¶
constant |
value |
unit |
|---|---|---|
u |
931.4941 |
(MeV) |
c |
2.99792458e8 |
(m/s) |
e |
1.60217663e-19 |
換算式¶
全エネルギー¶
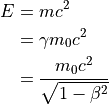
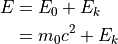
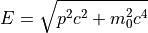
運動エネルギー¶
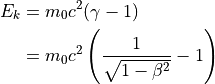
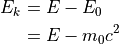
運動量¶
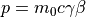
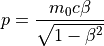
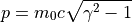
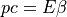
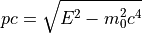
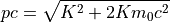
β、γの算出¶
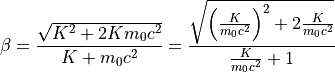
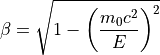
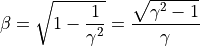
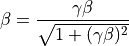
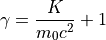
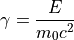
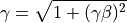
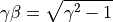
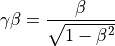
参考文献¶
Physics Memo : Koba-wiki ( https://www.rcnp.osaka-u.ac.jp/~kobayash/be_koba/cgi-bin/moin.cgi/Physics%20Memo.html )
