流体計算 ( Navier-Stokes Eq. )の基本式¶
基礎方程式 ( 圧縮性流れ )¶
Elmerモデルマニュアルにて記載されている基本式は次である.
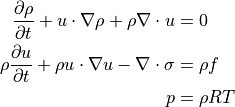
ここで、 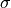 は圧力テンソル で、
は圧力テンソル で、 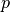 は圧力、
は圧力、 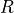 は理想気体の気体定数、
は理想気体の気体定数、  は流体温度である.これらは、ひずみ率テンソル
は流体温度である.これらは、ひずみ率テンソル  粘度
粘度 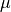 、比熱比
、比熱比 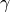 、等圧比熱
、等圧比熱 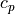 、等積比熱
、等積比熱 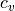 を用いて、以下の関係式が成り立つ.
を用いて、以下の関係式が成り立つ.
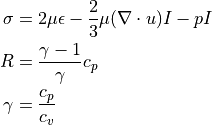
基本式を保存形式にて記述すると、
![\dfrac{ \partial \rho }{ \partial t } + \nabla \cdot ( \rho u ) &= 0 \\
\dfrac{ \partial }{ \partial t } ( \rho u ) + \nabla \cdot \left[ \rho u u - \sigma \right] &= \rho f \\
p &= \rho RT](../../../_images/math/7e0e72fd24515efe5e7cf6d58ce05c2f60b04cfa.png)
と、見通しの良い形に記述できる.
基礎方程式 ( 非圧縮 )¶
非圧縮の場合 (e.g.低圧下での水)、 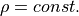 が成立する.このとき、質量保存則は、
が成立する.このとき、質量保存則は、
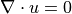
と簡略化できる.流れに発散がないため、流線の途中で流れが湧き出したりすることはない、
elmer 内の解くべき方程式は、以下となる.
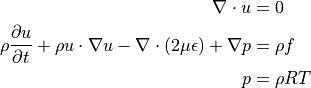
非圧縮流体の場合、圧力p は、スカラーポテンシャルの勾配としてのみ現れるため、 便宜上の値 であり、 実在の圧力値とは無関係の値として取り扱われる( 圧力p の値に物理的な意味はない ).
Note
"Re: pressure in Navier Stokes equations ( Post by raback » 24 Feb 2010, 20:43 ) Hi. If you study the incompressible N-S equation the pressure is there only behind a gradient operator. Hence the pressure field is defined only up to a constant. However, the standard weak formulation of Elmer sets the pressure to ~zero if the normal velocity component is not defined. So it is a true pressure pressure what you have. In compressible flows negative pressure would be certainly unphysical. -Peter"
Note
"非圧縮性N-S方程式の場合、圧力項は勾配演算子の後ろにのみ現れる.このため、圧力値は定数分の自由度が存在します.Elmerの標準的定式化の弱形式において、法線速度成分が定義されていない場合、圧力はゼロへと設定されます.そのため、正味の圧力(圧力差)のみが取り扱われていることになります.圧縮性流れにおいてであれば、負圧は確かに非物理的な値ですが、非圧縮の場合は便宜的な値を意味します. -Peter"
基礎方程式 ( 非圧縮 - Bousinesq近似 )¶
非圧縮の場合、密度は一定である.一方で、温度変化に伴って、流体には微小な体積膨張が発生する.本来、圧縮性流れの解析を要するが、これを非圧縮NS方程式において解くことを考える.体積膨張率を定数として密度の温度変化を線形化し、流体に働く浮力を外力とみなせば、比較的容易に温度上昇による体積膨張を含めた非圧縮流体解析が可能となる.これを Bousinesq近似 と呼ぶ.
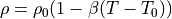
ここで、 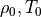 は基準となる密度、
は基準となる密度、 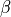 は基準温度における体積膨張率である.
は基準温度における体積膨張率である.
温度 T については、熱方程式 (HeatSolver)や移流拡散方程式(AdvectionDiffusionSolver)を用いて解く.
Reference¶
Elmer Discussion Forum. ( Pressure in Navier Stokes equations ) ( http://www.elmerfem.org/forum/viewtopic.php?t=329
Elmer Model Manual. ( https://www.nic.funet.fi/index/elmer/doc/ElmerModelsManual.pdf )
